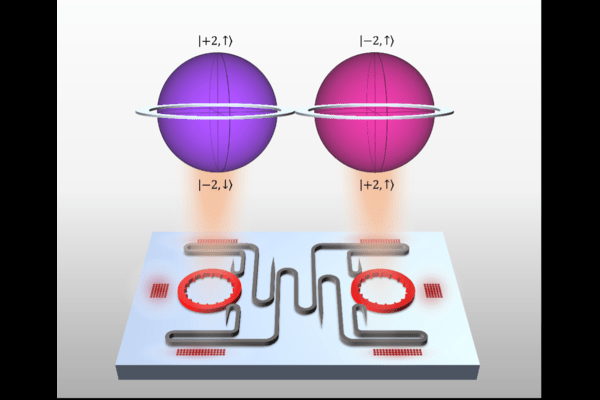
Researchers at Penn Engineering have created a chip that outstrips the security and robustness of existing quantum communications hardware. Their technology communicates in “qudits,” doubling the quantum information space of any previous on-chip laser.
Liang Feng, Professor in the Departments of Materials Science and Engineering (MSE) and Electrical Systems and Engineering (ESE), along with MSE postdoctoral fellow Zhifeng Zhang and ESE Ph.D. student Haoqi Zhao, debuted the technology in a recent study published in Nature. The group worked in collaboration with scientists from the Polytechnic University of Milan, the Institute for Cross-Disciplinary Physics and Complex Systems, Duke University and the City University of New York (CUNY).
Bits, Qubits and Qudits
While non-quantum chips store, transmit and compute data using bits, state-of-the-art quantum devices use qubits. Bits can be 1s or 0s, while qubits are units of digital information capable of being both 1 and 0 at the same time. In quantum mechanics, this state of simultaneity is called “superposition.”
A quantum bit in a state of superposition greater than two levels is called a qudit to signal these additional dimensions.
“In classical communications,” says Feng, “a laser can emit a pulse coded as either 1 or 0. These pulses can easily be cloned by an interceptor looking to steal information and are therefore not very secure. In quantum communications with qubits, the pulse can have any superposition state between 1 and 0. Superposition makes it so a quantum pulse cannot be copied. Unlike algorithmic encryption, which blocks hackers using complex math, quantum cryptography is a physical system that keeps information secure.”
Qubits, however, aren’t perfect. With only two levels of superposition, qubits have limited storage space and low tolerance for interference.
The Feng Lab device’s four-level qudits enable significant advances in quantum cryptography, raising the maximum secrete key rate for information exchange from 1 bit per pulse to 2 bits per pulse. The device offers four levels of superposition and opens the door to further increases in dimension.
“The biggest challenge,” says Zhang, “was the complexity and non-scalability of the standard setup. We already knew how to generate these four-level systems, but it required a lab and many different optical tools to control all the parameters associated with the increase in dimension. Our goal was to achieve this on a single chip. And that’s exactly what we did.”
The Physics of Cybersecurity
Quantum communication uses photons in tightly controlled states of superposition. Properties such as location, momentum, polarization and spin exist as multiplicities at the quantum level, each of which is governed by probabilities. These probabilities describe the likelihood of a quantum system—an atom, a particle, a wave—taking on a single attribute when measured.
In other words, quantum systems are neither here nor there. They are both here and there. It is only the act of observation—detecting, looking, measuring—that causes a quantum system to take on a fixed property. Like a subatomic game of Statues, quantum superpositions take on a single state as soon as they are observed, making it impossible to intercept them without detection or copy them.
The hyperdimensional spin-orbit microlaser builds on the team’s earlier work with vortex microlasers, which sensitively tune the orbital angular momentum (OAM) of photons. The most recent device upgrades the capabilities of the previous laser by adding another level of command over photonic spin.
This additional level of control—being able to manipulate and couple OAM and spin—is the breakthrough that allowed them to achieve a four-level system.
The difficulty of controlling all these parameters at once is what had been hindering qudit generation in integrated photonics and represents the major experimental accomplishment of the team’s work.
“Think of the quantum states of our photon as two planets stacked on top of each other,” says Zhao. “Before, we only had information about these planets’ latitude. With that, we could create a maximum of two levels of superposition. We didn’t have enough information to stack them into four. Now, we have longitude as well. This is the information we need to manipulate photons in a coupled way and achieve dimensional increase. We are coordinating each planet’s rotation and spin and holding the two planets in strategic relation to each other.”
Quantum Cryptography with Alice, Bob and Eve
Quantum cryptography relies on superposition as a tamper-evident seal. In a popular cryptography protocol known as Quantum Key Distribution (QKD), randomly generated quantum states are sent back and forth between sender and receiver to test the security of a communications channel.
If sender and receiver (always Alice and Bob in the storyworld of cryptography) discover a certain amount of discrepancy between their messages, they know that someone has attempted to intercept their message. But, if the transmission remains mostly intact, Alice and Bob understand the channel to be safe and use the quantum transmission as a key for encrypted messages.
How does this improve on non-quantum communication security? If we imagine the photon as a sphere rotating upwards, we can get a rough idea of how a photon might classically encode the binary digit 1. If we imagine it rotating downwards, we understand 0.
When Alice sends classical photons coded in bits, Eve the eavesdropper can steal, copy and replace them without Alice or Bob realizing. Even if Eve cannot decrypt the data she has stolen, she may be squirreling it away for a near future when advances in computing technology might allow her to break through.
Quantum communication adds a stronger layer of security. If we imagine the photon as a sphere rotating upwards and downwards at the same time, coding 1 and 0 simultaneously, we get an idea of how a qubit maintains dimension in its quantum state.
When Eve tries to steal, copy and replace the qubit, her ability to capture the information will be compromised and her tampering will be apparent in the loss of superposition. Alice and Bob will know the channel is not secure and will not use a security key until they can prove that Eve has not intercepted it. Only then will they send the intended encrypted data using an algorithm enabled by the qubit key.
However, while the laws of quantum physics may prevent Eve from copying the intercepted qubit, she may be able to disturb the quantum channel. Alice and Bob will need to continue generating keys and sending them back and forth until she stops interfering. Accidental disturbances that collapse superposition as the photon travels through space also contribute to interference patterns.
A qubit’s information space, limited to two levels, has a low tolerance for these errors.
To solve these problems, quantum communication requires additional dimensions. If we imagine a photon rotating (the way the earth rotates around the sun) and spinning (the way the earth spins on its own axis) in two different directions at once, we get a sense of how the Feng Lab qudits work.
If Eve tries to steal, copy and replace the qudit, she will not be able to extract any information and her tampering will be clear. The message sent will have a much greater tolerance for error—not only for Eve’s interference, but also for accidental flaws introduced as the message travels through space. Alice and Bob will be able to efficiently and securely exchange information.
“There is a lot of concern,” says Feng, “that mathematical encryption, no matter how complex, will become less and less effective because we are advancing so quickly in computing technologies. Quantum communication’s reliance on physical rather than mathematical barriers make it immune to these future threats. It’s more important than ever that we continue to develop and refine quantum communication technologies.”
This research was supported by the US Army Research Office (ARO) (W911NF-19-1-0249 and W911NF-21-1-0148), National Science Foundation (NSF) (ECCS-1932803, ECCS-1842612, OMA-1936276 and PHY-1847240), Defense Advanced Research Projects Agency (DARPA) (W91NF-21-1-0340), Office of Naval Research (ONR) (N00014-20-1-2558) and King Abdullah University of Science & Technology (OSR-2020-CRG9-4374.3). L.F. also acknowledges the support from Sloan Research Fellowship. This work was partially supported by NSF through the University of Pennsylvania Materials Research Science and Engineering Center (MRSEC) (DMR-1720530) and carried out in part at the Singh Center for Nanotechnology, which is supported by the NSF National Nanotechnology Coordinated Infrastructure Program under grant NNCI-1542153.
